Some AWGs and DACs use samples with a higher resolution than the DAC itself. The Tabor Proteus uses 16-bit samples while the DAC core is 14-bit. The advantage of this method is that SNR will be minimally affected by any calculations for any intermediate signal processing. For example, a common processing stage is an x/sin(x) digital filter that is usually applied before data conversion to flatten the frequency response. Using higher resolution samples means “calculation noise” will not affect the validity of any of the actual bits being applied to the DAC.
Other real-time processing would also result in the loss of effective bits with respect to the input signals. Interpolation, for example, see Figure 2.1: Oversampling (interpolating) DACs are common as they can increase the Nyquist BW, moving the nearest out of the band of interest, or they can spread the quantization noise over a larger BW, thus reducing the noise density.
Oversampling is like increasing the number of bits, you get one additional bit every time the sampling rate is multiplied by four. However, to achieve a processing gain like this the input samples must have a resolution equal to or better than the improved resolution. Let us look at how an interpolator works; Interpolators take the input sequence of samples, insert zeros to increase the sampling rate (zero-padding), and then apply a sharp roll-off LPF to get rid of the unwanted images. As input signals are finite resolution integers, these are already carrying the quantization noise corresponding to the integer length being used over the non-interpolated sample rate Nyquist band. Zero-padding will result in the replication of the spectrum of the signal over the new Nyquist band, including the original quantization noise. The final Low-Pass filter will add some additional calculation noise. Yielding little or no improvement to the SNR.
As mentioned earlier the Tabor Proteus architecture uses 16 bits samples, and interpolation capability up to 16x (2 bits), and utilizes a 14 bit DAC, so it can take advantage of processing gain with improved SNR. The same considerations apply to other signal processing blocks such as DUC (Digital-Up-Converters) and I/Q modulators where interpolation and real time arithmetic are also applied. When higher resolution samples are not used in interpolation it is the equivalent of losing effective bits from the DAC. If 14-bit input samples would be used in Proteus, then the output of the DAC would be equivalent to using a 12-bit DAC when interpolating by 16x.
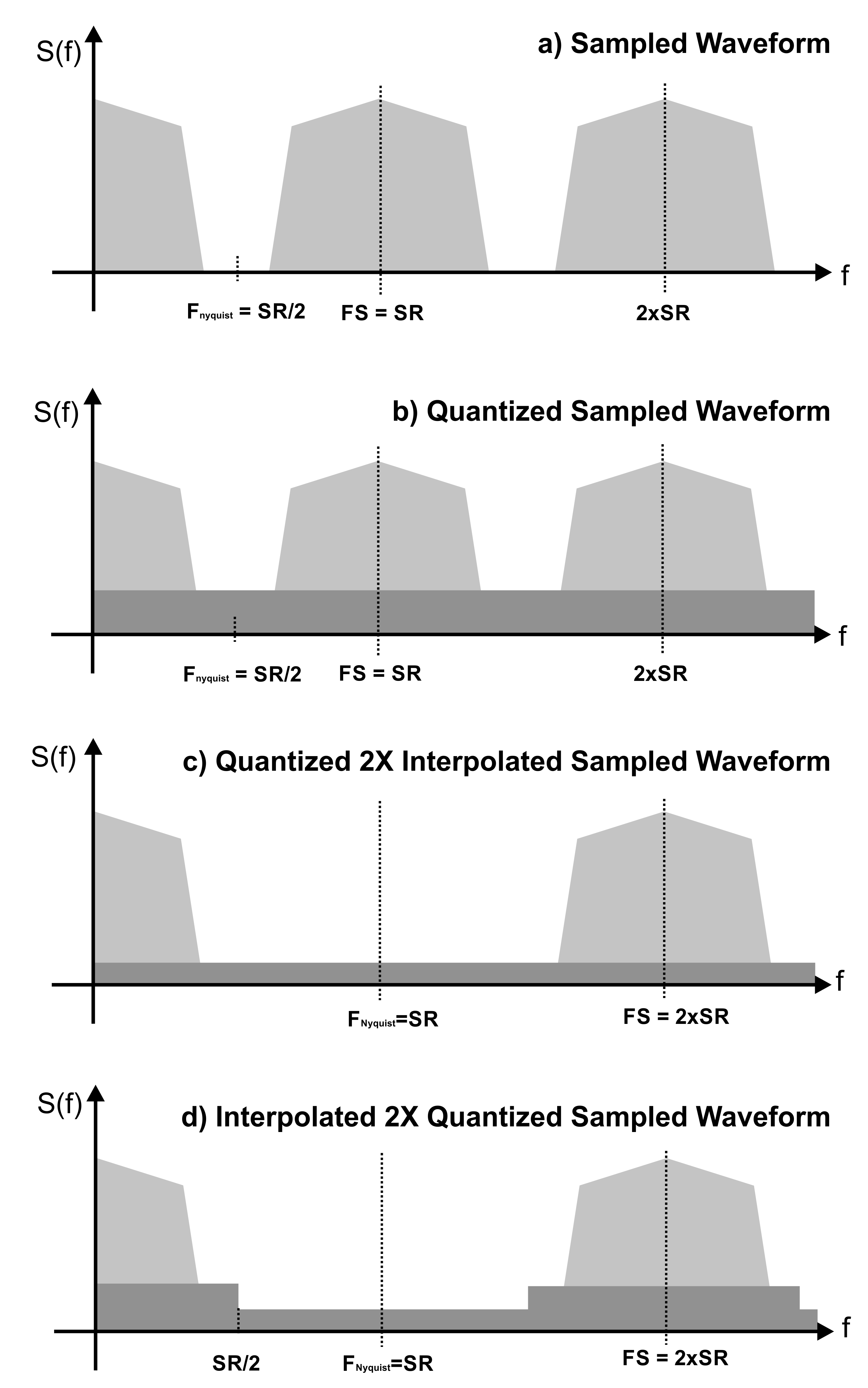
Figure 2.1: Sample resolution may become important when using DSP techniques to improve the behavior of an AWG. Interpolation is one of these cases. In the above example, a signal is calculated and stored with a high accuracy (a). When this signal is generated by an AWG, quantization noise will be added to it(b). If the signal is ideally interpolated (x2 in this example), the same quantization noise will be spread over a higher bandwidth so the SQNR will improve (c). However, if the signal is stored with the resolution of the DAC before being interpolated, quantization noise will be also interpolated so the SQNR will be kept and no processing-gain will be obtained (d). The Tabor Proteus uses 16-bit samples although the DAC is 14-bit for this specific reason.
Fore more information: [email protected]